Lec 5 Building Cognitive Networks with BrainCog

Introduction

Cognitive models are designed to perform various cognitive functions. In BrainCog, we provide a complete set of interface components for building models. BrainCog allows users to freely and easily create the required networks and corresponding functions by calling and connecting the base modules.

There are three main components to build a network:

node: used to declare the neuron group containing the commonly used models such as IF LIF HH IZH
connection: used to define the connections between neuron groups
learningrule: used to define the the learning rule to adjust weights of the learned connections

Brainarea

To build models that exhibits full functionality, we should conbine above components. Such a model, we called Brainarea, is minimal basic module which have full functionality. All cognitive models are excepted to inherit class BrainArea(nn.Module, abc.ABC)

Import

In order to use these three components, we should first import these modules.

import torch
from braincog.base.node import *
from braincog.base.learningrule import *
from braincog.base.connection import *
from braincog.base.brainarea import *

Construction of Models

In this section, We will build a feedback network. It has two groups of neurons. As shown in figure below, the first group recieve both input from outside and output from second group. And the second group recieve output from first group, and output to outside and first group.

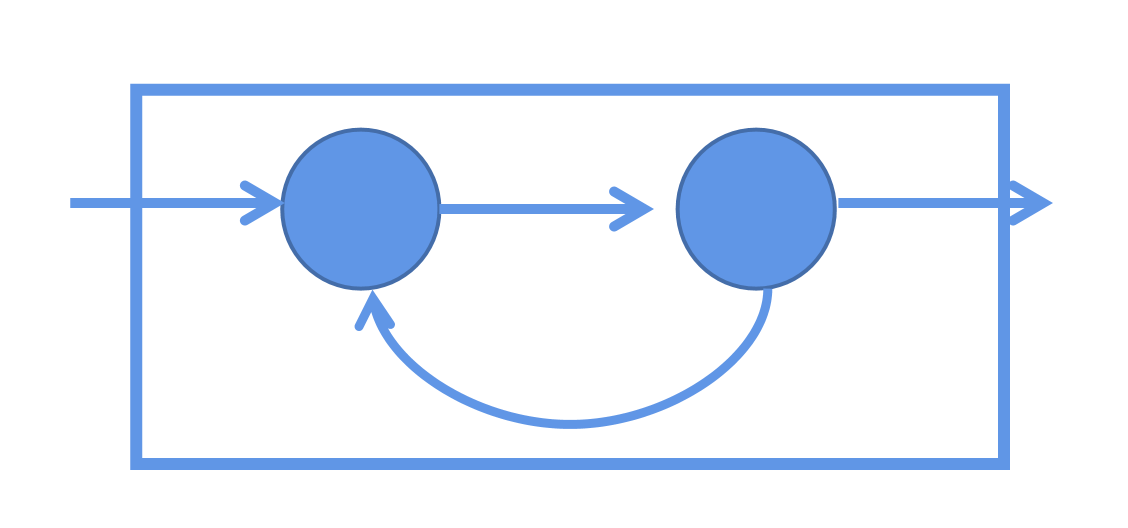
1. Neuron Group

We first declare the neurons. We choose IF neuron as our basic neural type.

node = [IFNode(threshold=1.), IFNode(threshold=1.)]
print(node)

one IFNode() represents one group of neurons. The exact number of neurons in one group depends on the dimension of input. threshold is optical parameter and it defaults to 1.

2. Connection

Then we declare the connection. Usually, connection needs a weight matrix and a mask: CustomLinear(w,mask=None) . Weight matrix is a adjacency matrix between two neuron groups which connected by this connection. mask is excepted to be binary matrix which represents if this connetion is exist. If you do not need a mask in your code or it is fully connected, just set to None.

Here, we declare three connections, which represent input weight of the first group, input weight of the second group, and weight of feedback connection , respectly .

w1 = torch.tensor([[1., 1], [1, 1]])
w2 = torch.tensor([[1., 1], [1, 1]])
w3 = torch.tensor([[0.4, 0.4], [0.4, 0.4]])
connection = [CustomLinear(w1), CustomLinear(w2), CustomLinear(w3)]
print(connection)

3. Learning rule

Next, we combine node and connection with learning rule.

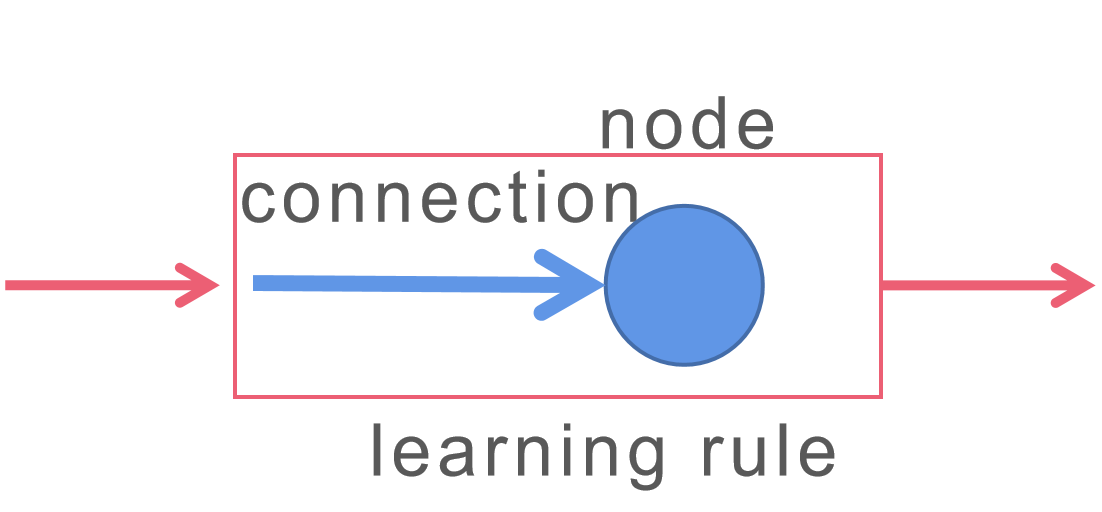
Usually, as shown in figure above, learning rule defines the relationship between node and connection. It link them by parameter transmission when declare a learning rule instance. Also, you directly pass the connection’s output to node, but you would not get variation of the weight.

stdp = []

stdp.append(MutliInputSTDP(node[0], [connection[0], connection[2]]))
stdp.append(STDP(node[1], connection[1]))
print(stdp)

A learning rule only care about which node connection link to. The node before the connection would not affect the calculation of variation of weight.

4. Link module

Up to now, we have constructed serval basic module. Now we begin to link all these basic module to a network.

x=torch.tensor([[0.1, 0.1]]) 
x1 = torch.zeros(1, w3.shape[0])
x, dw1 = stdp[0](x, x1)
x1, dw2 = stdp[1](x)
print(x1)

By calling the forward funtion, we can obtain both output and variation of weight. We call each forward funtion orderly and get all the outputs.

5. Define our brainarea class

We put all the code in a class called “Feedback”.

class Feedback(BrainArea):


    def __init__(self, w1, w2, w3):
        """
        """
        super().__init__()

        self.node = [IFNode(), IFNode()]
        self.connection = [CustomLinear(w1), CustomLinear(w2), CustomLinear(w3)]
        self.stdp = []

        self.stdp.append(MutliInputSTDP(self.node[0], [self.connection[0], self.connection[2]]))
        self.stdp.append(STDP(self.node[1], self.connection[1]))
        self.x1 = torch.zeros(1, w3.shape[0])

    def forward(self, x):

        x, dw1 = self.stdp[0](x, self.x1)
        self.x1, dw2 = self.stdp[1](x)

        return self.x1, (*dw1, *dw2)

    def reset(self):
        self.x1 *= 0

T = 20
w1 = torch.tensor([[1., 1], [1, 1]])
w2 = torch.tensor([[1., 1], [1, 1]])
w3 = torch.tensor([[-0.4, -0.4], [-0.4, -0.4]])
ba = Feedback(w1, w2,w3)
for i in range(T):
    x = ba(torch.tensor([[0.1, 0.1]]))
    print(x[0])

We run this model T steps. And we get T outputs.